疾患と検査の関係(感度・特異度・陽性的中率・陰性的中率)
Twitterでもつぶやいていた内容のまとめをブログでします.
内容は疾患と検査の関係についてどのように考えるのかについてです.
参考にしたのは『第23回 診断精度の指標とROC - 核医学文献情報研究会』です.
疾患と検査には以下の表のような関係があります.
また,疾患と検査の関係はベン図で以下のように表わすこともできます.
疾患と検査の関係を表す指標である感度・特異度・陽性的中率・陰性的中率について考察していきます.
感度sensitivity
疾患と検査の関係表からわかるように感度とは疾患有のうち検査陽性になる割合を表したものです.
いいかえれば,疾患が有ることを正しく陽性といえた割合です.
このことを条件付き確率で表せば
となります.
特異度specificity
疾患と検査の関係表からわかるように特異度とは疾患無のうち検査陰性になる割合を表したものです.
いいかえれば,疾患が無いことを正しく陰性といえた割合です.
このことを条件付き確率で表せば
となります.
陽性的中率positive predictive value
疾患と検査の関係表からわかるように陽性的中率とは検査陽性のうち疾患有になる割合を表したものです.
いいかえれば,検査が陽性であることが正しく疾患が有るといえた割合です.
陽性的中率ではベイズの定理を用いて
となることから
陽性的中率=感度×有病率/(感度×有病率+(1−有病率)(1−特異度))
によって求められることがわかります.
陰性的中率negative predictive value
疾患と検査の関係表からわかるように陰性的中率とは検査陰性のうち疾患無になる割合を表したものです.
いいかえれば,検査が陰性であることが正しく疾患が無いといえた割合です.
陰性的中率ではベイズの定理を用いて(途中省略)
となることから
陰性的中率=特異度 × (1−有病率) / (特異度×(1−有病率) + 有病率×(1−感度))
によって求められることがわかります.
有病率によって変化する陽性的中率と陰性的中率
検査の感度と特異度をどのように決定するかは検査をする側にとって大きな問題になります.
このことについては先にあげた参考サイトにROC曲線を用いた説明があります.
そこでここでは検査をされる側の視点に立って感度と特異度がわかっている検査において陽性的中率と陰性的中率がどのように変化するかを考えます.
陽性的中率と陰性的中率のそれぞれの式からわかるように両者は有病率に依存します.
どのような形で依存するのかをグラフで示してみます.
つぎのグラフは感度99.1%,特異度99.5%という大変優れた検査精度を仮定したときに有病率を0〜5%まで変化させたときのものになります.
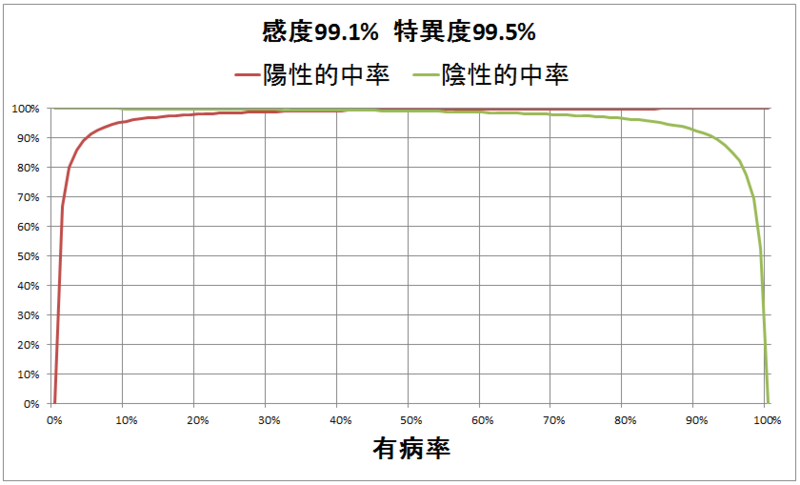
全体像を見るために感度99.1%,特異度99.5%という検査精度を仮定したときに有病率を0〜100%まで変化させたときのグラフも示します.
検査精度(感度・特異度)を向上させた場合でも
- 有病率が低い場合には,陽性的中率も低く・陰性的中率は高くなる傾向
- 有病率が高い場合には,陽性的中率も高く・陰性的中率は低くなる傾向
であることがグラフから読み取れます.
感度と精度を変化させてもっと実感できるようにCASIOが提供している高精度計算サイトに以下の自作式を作りました.